A scattering angle of 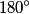$180^{\circ}$ means that an alpha particle will travels directly toward a nucleus, comes to a complete halt as it approaches the nucleus, and then turns around and starts moving directly away from the nucleus. At the time when the alpha particle comes to a complete halt, all of its kinetic energy will have been converted into potential energy. Therefore, fi we let r denote the distance between the alpha particle and nucleus at this moment, then
$\begin{align*}5\cdot 10^6 \mbox{ eV} = \frac{2\cdot 50 e^2}{4 \pi \epsilon_0 r}\end{align*}$
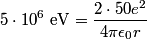This can be easily solved for $r$ , yielding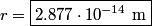
$\begin{align*}r = \boxed{2.877 \cdot 10^{-14} \mbox{ m}}\end{align*}$
Therefore, answer (B) is correct.

Solution to 1996 Problem 19